Free surface outlets, also referred to as perched or free fall outlets, exist when the tailwater does not influence the water depth within the culvert outlet.  The method used by FishXing to addresses free surface outlets depends on the hydraulic slope of the culvert.

Steep Culverts

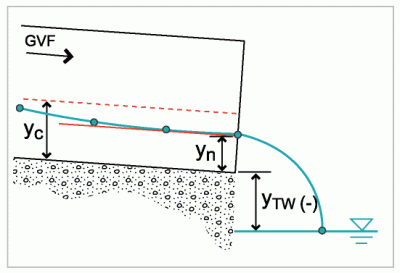
At hydraulically steep slopes (yn < yc), if the tailwater is below critical depth (y_tw < y_c) supercritical flow will occur throughout the culvert.  In this case, the controlling water depth is at the upstream end of the culvert.  If the tailwater depth is below the culvert outlet bottom (y_tw < 0) the culvert is considered perched.  Under supercritical flow conditions, FishXing assumes the water depth at the perched culvert outlet is not influenced by the free overfall.

Non-steep Culverts

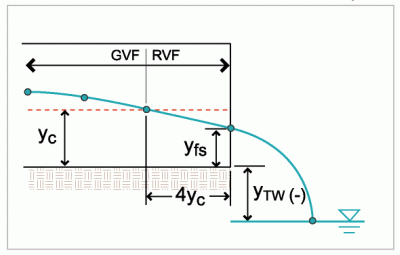
For culverts with a hydraulic slope that is not steep (instead having either a mild, critical, horizontal, or adverse slope) and having a perched culvert outlet (y_tw < 0) , the water surface profile will be on a draw-down curve as it approaches the free overfall. From where the profile crosses through critical depth to the free outfall the flow enters into a rapidly varied flow regime. Rouse (1936) examined the case of an overfall at the end of a mild slope and found that the true critical section is located at the overfall crest. The depth of this crest is a function of the wetted area at the computed critical depth, y_c:

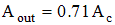
The exact location of the calculated critical depth is indeterminate, as it will move upstream with increasing flow and downstream with increasing boundary roughness and surface slope. For relatively smooth rectangular channels, Rouse found this distance approximately equal to four times the critical depth (4y_c) upstream from the crest.

For non-steep culvert with a free overfall FishXing approximates the water surface profile near the outlet by assuming the water depth is equal to critical depth a distance of 4yc upstream of the outlet.  FishXing then assumes the free surface depth located at the outlet (Y_fs) is a function of 0.71Ac.  The water surface is then assumed to be linear between yc and y_fs.