Continuity Equation |
One of the fundamental principles used in the analysis of uniform flow is known as the Continuity of Flow. This principle is derived from the fact that mass is always conserved in fluid systems regardless of the pipeline complexity or direction of flow.
If steady flow exists in a channel and the principle of conservation of mass is applied to the system, there exists a continuity of flow, defined as: "The mean velocities at all cross sections having equal areas are then equal, and if the areas are not equal, the velocities are inversely proportional to the areas of the respective cross sections." Thus if the flow is constant in a reach of channel the product of the area and velocity will be the same for any two cross sections within that reach. Looking a the units of the product of area (sq-ft) and velocity (fps) leads to the definition of flow rate (cfs). This is expressed in the Continuity Equation:
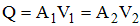
Where:
Q = the volumetric flow rate
A = the cross sectional area of flow
V = the mean velocity
Calculation of flow rate is often complicated by the interdependence between flow rate and friction loss. Each affects the other and often these problems need to be solved iteratively. Once flow and depth are know the continuity equation is used to calculate velocity in the culvert.
Note: This principle can be used to describe the drop in water surface at a culvert inlet. For example, when the flow is constant and the water velocity increases due to a decrease in roughness, such as through a culvert, the flow area must decrease. In the case of constant cross section geometry that change in area is reflected in a change in the water surface elevation. Q=VA, when flow is constant, as velocity increases, the flow area decreases and vice versa.
See also: Manning's Equation, Open Channel Flow